# 探索Circle STARKs近年来,STARKs协议设计的趋势是转向使用较小的字段。最早期的STARKs生产实现使用的是256位字段,即对大数字进行模运算。但这种设计效率较低,处理大数字会浪费很多算力。为解决这个问题,STARKs开始使用更小的字段:首先是Goldilocks,然后是Mersenne31和BabyBear。这种转变大幅提升了证明速度。例如Starkware现在能在一台M3笔记本上每秒证明620,000个Poseidon2哈希。这意味着只要我们信任Poseidon2作为哈希函数,就可以解决高效ZK-EVM开发的难题。那么这些技术是如何工作的?小字段上的证明如何构建?本文将探讨这些细节,特别关注Circle STARKs这种与Mersenne31字段兼容的方案。## 使用小字段时的常见问题在创建基于哈希的证明时,一个重要技巧是通过证明多项式在随机点的评估来间接验证多项式性质。这可以大大简化证明过程。例如,假设协议要求你生成一个多项式A的commitment,满足A^3(x) + x - A(ωx) = x^N。协议可以要求你选择随机坐标r并证明A(r)^3 + r - A(ωr) = r^N。然后反推A(r) = c,你证明Q = (A - c)/(X - r)是一个多项式。为防止攻击,我们需要在攻击者提供A后再选择r。在基于椭圆曲线的协议中,这很简单:我们可以选择一个随机的256位数字作为r。但在小字段STARKs中,只有约20亿个r可选,攻击者可能通过穷举破解。这个问题有两个解决方案:1. 进行多次随机检查2. 扩展字段多次随机检查简单有效,但可能存在效率问题。扩展域类似于复数,但基于有限域。我们引入新值α,声明α^2=某个值。这样创建了一个新的数学结构,能在有限域上进行更复杂的运算。通过扩展域,我们有了足够多的值来选择,满足安全需求。大部分数学运算仍在基础字段上进行,只在需要增强安全性时使用更大的字段。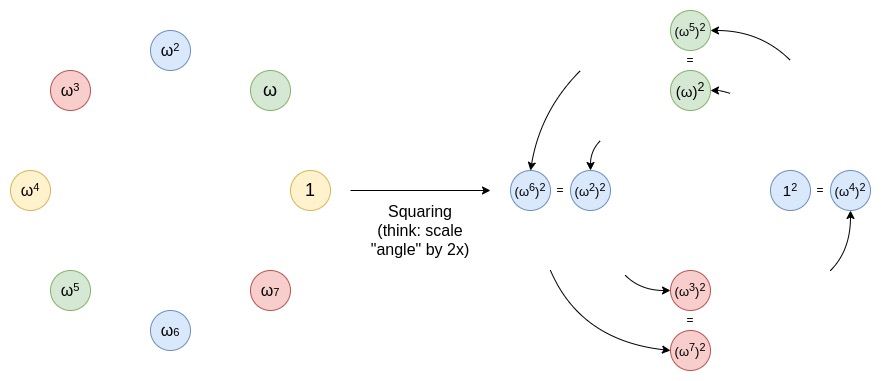## Regular FRIFRI (Fast Reed-Solomon Interactive)协议是构建SNARK或STARK的重要步骤。它通过将证明多项式度数为d的问题简化为证明度数为d/2的问题来简化验证过程。这个过程可以重复多次,每次都将问题简化一半。FRI的工作原理是重复简化过程。从证明多项式度数为d开始,通过一系列步骤,最终证明度数为d/2。每次简化后,生成的多项式度数逐步减小。如果某个阶段输出不符合预期,那一轮检查将失败。为实现域的逐步减少,使用了二对一映射。这种映射允许将数据集大小减半,同时保留相同属性。这种操作可以想象成将圆周上的线段沿圆周伸展两圈的过程。为使映射技术有效,原始乘法子群的大小需要有大的2的幂作为因子。BabyBear的模数使其最大乘法子群包含所有非零值,非常适合此技术。Mersenne31的乘法子群大小只有一个2的幂因子,限制了其应用范围。Mersenne31域非常适合在32位CPU/GPU上进行算术运算,比BabyBear域快约1.3倍。如果能在Mersenne31域中实现FRI,将显著提升计算效率。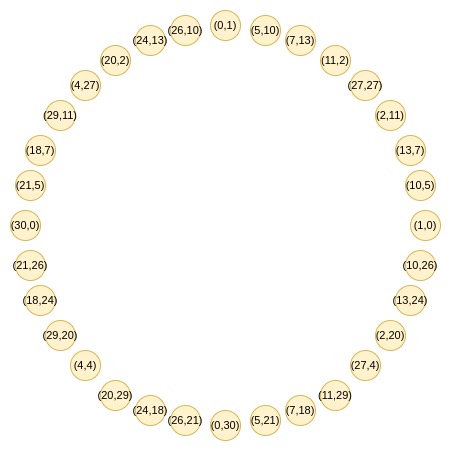## Circle FRICircle STARKs的巧妙之处在于,给定质数p,可以找到大小为p的群体,具有类似的二对一特性。这个群体由满足特定条件的点组成,如x^2 mod p等于某值的点集。这些点遵循加法规律:(x1,y1) + (x2,y2) = (x1x2 - y1y2, x1y2 + x2y1)双倍形式是:2 * (x,y) = (2x^2 - 1, 2xy)Circle FRI首先将所有点收敛到一条直线上,然后进行随机线性组合得到一维多项式P(x)。从第二轮开始,映射变为:f0(2x^2-1) = (F(x) + F(-x))/2这个映射每次将集合大小减半,将圆上两个相对点的x坐标转换为倍增后点的x坐标。这本可以在二维空间完成,但一维操作更高效。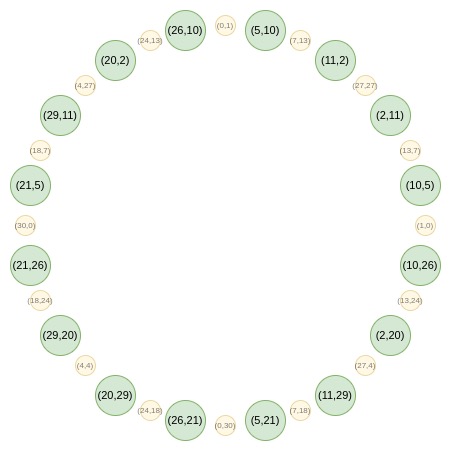## Circle FFTsCircle group也支持FFT,构造方式与FRI类似。Circle FFT处理的对象是Riemann-Roch空间,而不是严格的多项式。Circle FFT输出的系数是特定于Circle FFT的基础。作为开发者,你几乎可以完全忽略这一点。STARKs只需将多项式作为评估值集合存储。唯一需要FFT的地方是进行低度扩展:给定N个值,生成k*N个同一多项式上的值。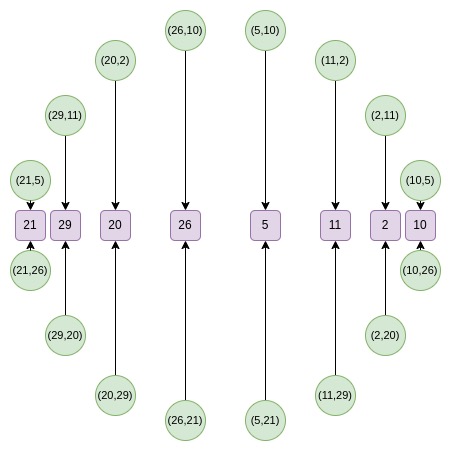## Quotienting在Circle STARKs中,由于没有可以通过单点的线性函数,需要采用不同技巧替代传统商运算。我们不得不通过在两点上评估来证明,添加一个虚拟点。如果多项式P在x1处等于y1,在x2处等于y2,我们选择插值函数L,在这两点相等。然后证明P-L在两点为零,通过L除以L来证明商Q是多项式。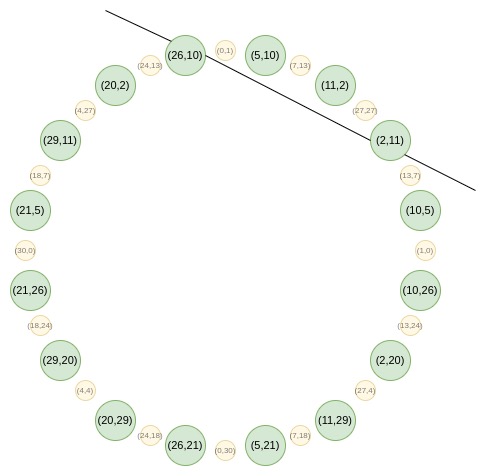## Vanishing polynomials在Circle STARKs中,消失多项式为:Z1(x,y) = yZ2(x,y) = xZn+1(x,y) = (2 * Zn(x,y)^2) - 1这可以从折叠函数推导:在Circle STARKs中重复使用x → 2x^2 - 1。第一轮需要特殊处理。## Reverse bit orderCircle STARKs使用修改的反向位序,反转除最后一位的每一位,用最后一位决定是否翻转其他位。这反映了Circle STARKs特有的折叠结构。## 效率Circle STARKs非常高效。计算通常涉及:1. 原生算术:用于业务逻辑2. 原生算术:用于加密学(如Poseidon哈希) 3. 查找参数:通过表查值实现各种计算Circle STARKs充分利用了计算空间,浪费较少。比Binius稍逊,但概念更简单。## 结论Circle STARKs对开发者来说并不比常规STARKs复杂。理解Circle FRI和FFTs可以帮助理解其他特殊FFTs。目前STARKs基础层效率接近极限,未来优化方向可能包括:1. 最大化哈希函数和签名的算术化效率2. 递归构造以提高并行化3. 算术化虚拟机以改善开发体验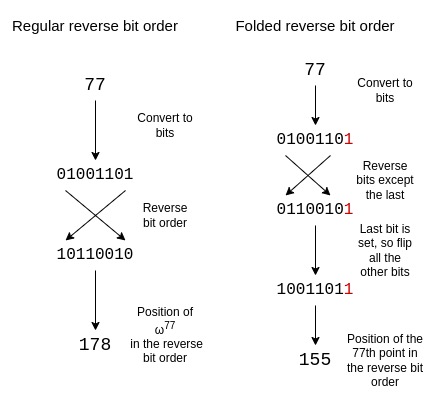
Circle STARKs: 小字段高效ZK证明的探索与突破
探索Circle STARKs
近年来,STARKs协议设计的趋势是转向使用较小的字段。最早期的STARKs生产实现使用的是256位字段,即对大数字进行模运算。但这种设计效率较低,处理大数字会浪费很多算力。为解决这个问题,STARKs开始使用更小的字段:首先是Goldilocks,然后是Mersenne31和BabyBear。
这种转变大幅提升了证明速度。例如Starkware现在能在一台M3笔记本上每秒证明620,000个Poseidon2哈希。这意味着只要我们信任Poseidon2作为哈希函数,就可以解决高效ZK-EVM开发的难题。那么这些技术是如何工作的?小字段上的证明如何构建?本文将探讨这些细节,特别关注Circle STARKs这种与Mersenne31字段兼容的方案。
使用小字段时的常见问题
在创建基于哈希的证明时,一个重要技巧是通过证明多项式在随机点的评估来间接验证多项式性质。这可以大大简化证明过程。
例如,假设协议要求你生成一个多项式A的commitment,满足A^3(x) + x - A(ωx) = x^N。协议可以要求你选择随机坐标r并证明A(r)^3 + r - A(ωr) = r^N。然后反推A(r) = c,你证明Q = (A - c)/(X - r)是一个多项式。
为防止攻击,我们需要在攻击者提供A后再选择r。在基于椭圆曲线的协议中,这很简单:我们可以选择一个随机的256位数字作为r。但在小字段STARKs中,只有约20亿个r可选,攻击者可能通过穷举破解。
这个问题有两个解决方案:
多次随机检查简单有效,但可能存在效率问题。扩展域类似于复数,但基于有限域。我们引入新值α,声明α^2=某个值。这样创建了一个新的数学结构,能在有限域上进行更复杂的运算。
通过扩展域,我们有了足够多的值来选择,满足安全需求。大部分数学运算仍在基础字段上进行,只在需要增强安全性时使用更大的字段。
Regular FRI
FRI (Fast Reed-Solomon Interactive)协议是构建SNARK或STARK的重要步骤。它通过将证明多项式度数为d的问题简化为证明度数为d/2的问题来简化验证过程。这个过程可以重复多次,每次都将问题简化一半。
FRI的工作原理是重复简化过程。从证明多项式度数为d开始,通过一系列步骤,最终证明度数为d/2。每次简化后,生成的多项式度数逐步减小。如果某个阶段输出不符合预期,那一轮检查将失败。
为实现域的逐步减少,使用了二对一映射。这种映射允许将数据集大小减半,同时保留相同属性。这种操作可以想象成将圆周上的线段沿圆周伸展两圈的过程。
为使映射技术有效,原始乘法子群的大小需要有大的2的幂作为因子。BabyBear的模数使其最大乘法子群包含所有非零值,非常适合此技术。Mersenne31的乘法子群大小只有一个2的幂因子,限制了其应用范围。
Mersenne31域非常适合在32位CPU/GPU上进行算术运算,比BabyBear域快约1.3倍。如果能在Mersenne31域中实现FRI,将显著提升计算效率。
Circle FRI
Circle STARKs的巧妙之处在于,给定质数p,可以找到大小为p的群体,具有类似的二对一特性。这个群体由满足特定条件的点组成,如x^2 mod p等于某值的点集。
这些点遵循加法规律:(x1,y1) + (x2,y2) = (x1x2 - y1y2, x1y2 + x2y1) 双倍形式是:2 * (x,y) = (2x^2 - 1, 2xy)
Circle FRI首先将所有点收敛到一条直线上,然后进行随机线性组合得到一维多项式P(x)。从第二轮开始,映射变为:f0(2x^2-1) = (F(x) + F(-x))/2
这个映射每次将集合大小减半,将圆上两个相对点的x坐标转换为倍增后点的x坐标。这本可以在二维空间完成,但一维操作更高效。
Circle FFTs
Circle group也支持FFT,构造方式与FRI类似。Circle FFT处理的对象是Riemann-Roch空间,而不是严格的多项式。Circle FFT输出的系数是特定于Circle FFT的基础。
作为开发者,你几乎可以完全忽略这一点。STARKs只需将多项式作为评估值集合存储。唯一需要FFT的地方是进行低度扩展:给定N个值,生成k*N个同一多项式上的值。
Quotienting
在Circle STARKs中,由于没有可以通过单点的线性函数,需要采用不同技巧替代传统商运算。我们不得不通过在两点上评估来证明,添加一个虚拟点。
如果多项式P在x1处等于y1,在x2处等于y2,我们选择插值函数L,在这两点相等。然后证明P-L在两点为零,通过L除以L来证明商Q是多项式。
Vanishing polynomials
在Circle STARKs中,消失多项式为: Z1(x,y) = y Z2(x,y) = x Zn+1(x,y) = (2 * Zn(x,y)^2) - 1
这可以从折叠函数推导:在Circle STARKs中重复使用x → 2x^2 - 1。第一轮需要特殊处理。
Reverse bit order
Circle STARKs使用修改的反向位序,反转除最后一位的每一位,用最后一位决定是否翻转其他位。这反映了Circle STARKs特有的折叠结构。
效率
Circle STARKs非常高效。计算通常涉及:
Circle STARKs充分利用了计算空间,浪费较少。比Binius稍逊,但概念更简单。
结论
Circle STARKs对开发者来说并不比常规STARKs复杂。理解Circle FRI和FFTs可以帮助理解其他特殊FFTs。目前STARKs基础层效率接近极限,未来优化方向可能包括: